基礎の遺伝疫学講座   安田　徳一　(2008/10/20)

4. 二人の血縁者

　因子結合表現型システムは別として、個人単位のデータには原因を示す仮説についての情報はあまりないのであるが、それより若干ましな2人一組の血縁者単位のデータ取れる。このようなデータは比較的集め易いが、家系からの一組の血縁者(対)にみられる相関や再起リスクはあまり顕著でない。それにデータの集め方次第で何らかの偏りが生じ易いが、不完全確認incomplete ascertainmentなどの仮定は懸念する必要はない。

4.1. 条件確率

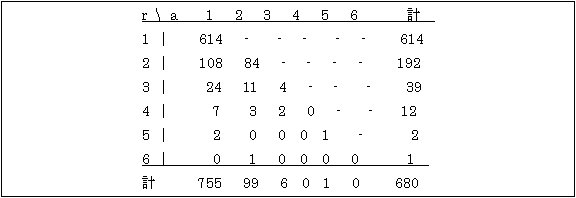
　二人の血縁者X、Yを考えよう。最も簡単な例として、それぞれが完全に無作為に選び出されたとする。Xを選んだ後Yを選ぶ条件確率は 

　　　　　　　　　　　　P(Y|X)=P(X,Y)/P(X) 

と表すことができる。量的形質XとYが二変量正規分布に従うなら、これは平均ρ、分散1-ρ²の1変量正規分布で表わすことができる。ここでρは標準化した変量XとY の母相関係数である。s人の構成員がいる家系の確率も多変量正規分布を仮定することで(複数の)相関係数を用いて表すことができる。

　遺伝疫学での特異的な問題の一つに標本の集め方が不完全選抜incomplete selectionになることが挙げられる。それは家族の確認方法として、患者のいない家族は無意識にデータから除外していることである。データの分析を考える上で発端者probandという考え方が導入されている。発端者は他の血縁者に関わりなく無作為に見つかる患者である。この最初にみつかった患者によりその家系が標本として取り上げられる。換言すれば発端者によって問題の家系が見つかる。発端者のいる家系で次ぎにみつかる患者は第二症例として区別する。同一家系に発端者が2名以上のこともある。きょうだいが離れて住んでいるとそれぞれの患者は別の医師の診察を受けることになる場合がある。病院記録、死亡小表、医師のカルテ、集団検診、そのほか症状(表現型)を確認するascertainedどんな手段でもよい。問診の過程でその家系の同胞であることが分かるであろう。データを集める際、丁寧にその過程を記録することが大切である。

家系図を描くとき発端者は左下から斜め上に向う矢印を付けて第二症例と区別する。最初の発端者を特にpropositus(指標者index case)ということがあるが、第二症例との違いに配慮しないと遺伝様式を決める分離比の推定で偏りが生じる重大な過ちを冒すことになる(第5章)。

　発端者の考えはただちに確認の確率πascertainment probabilityと結びつく。ある有限母集団において患者がR人いて、そのうちA人が発端者であったとする。確認の確率は

　　　　　　　　　　　　　　　　π=A/R 

で定義される。多くの不完全選抜の場合、推定値は必須であり、分離比の推定segregation frequency、再発リスクrecurrence riskの不偏推定値、それに集団の患者数の推定でπの推定値は必須である。すなわち、πの不偏推定値が求められれば 

　　　　　　　　　　　　　　　　R=A/π 

と発端者数から患者数が推定できる。そうすると集団での発生率はR/N、ここにNは集団の大きさである。π=1のとき、切れた選抜truncated selectionという。このとき、家系あたりの患者数が1人の場合と複数人いる場合とで、家系が選抜される確率は同じである。“切れた”という用語は、各家系での再起リスクが一定のとき患者数の分布が切れた二項分布となることによる。切れたという用語は患者のいない家系を除いて無作為抽出をする状況を反映する。

　π→0の状況を単独選抜single selectionという。ある家系が確認される確率は家系内の患者数に比例する状況を表す。これは不完全確認の最も簡単な場合で、血縁者の対や家系を分析するのに向いているが、次の2つの理由で避けるべきである。

1． π→0のとき、集団の患者数を求めることができない。

2． 単独確認では単離例isolated caseの判断が難しくなる。単離例は本来、多発例にもかかわらず子ども数が少ないために観察されたのか、あるいは他の原因(環境要因、表現模写phenocopy、突然変異などの他の遺伝機構)による弧発例sporadic caseと区別できない。

一般に0＜π＜1のときは複合選抜multiple selectionという。患者の症状が軽症で医師の注意を引かない、あるいは重症で早期に死亡していると、相当長い期間にわたって集中的な調査を行なってもおそらく切れた(完全)確認選抜(π=1)までにはならないであろう。

　X(発端者)とY(第二症例)はお互いに血縁があるとする。m_kをある診断基準kで患者であるリスク、f_kをXの血縁者の症状に関係なく、Xの年齢、性、その他の特徴で定まる先験的リスクとする。Xの罹患リスクは 

　　　　　　　　　　　　　　　　m_x=��f_k m_k 

と表せる。同様にしてXの診断基準がkであるときYが患者である確率をp_kとする。血縁者対(X, Y)に定義される再発リスクはXが患者であるとき、Yが患者である条件確率で次のように表せる。 

　　　　　　　　　　　　p_y|x = ��f_km_k p_k /��f_km_k 。 

例えば、完全浸透の劣性遺伝子ではf_kは4通りの交配型AA×−, Aa×Aa, Aa×aa, aa×aaそれぞれの確率で、(m_k)はそれぞれの交配型から劣性個体aaがそれぞれ分離する割合(分離比segregation frequency)0, 1/4, 1/2, 1である。 さらには診断基準kとして、新生突然変異、環境因子、他の遺伝子座の遺伝子型などを含めることがある。

　19世紀の初頭にメンデルの法則が再発見されてまもなく、ワインベルグ(Weinberg,1912)は複合選抜で同胞における再発リスクの推定値を求めた。 

         　　　　　　　  p_y|x = ��a(r-1)/��s(r-1) 

 sはきょうだいの大きさ、rは患者の数、そしてaは発端者数で、�狽ﾍ各同胞について加える。この推定値には偏りはないが、有効ではないためフィッシャー(Fisher  1934, 解説 Crow 1965)は有効推定量を求めている。 

　　　　　　　　　　　　p_y|x = ��Ca(r-1)/��Cs(r-1) 

ここで　1/C=1+π+ p_y|xπ(s-3) である。ここでπ=��a(a-1)/��a(r-1)である。

例題4.1.1.きょうだい二人に聴覚障害がある組のデータがある( Furusho & Yasuda 1973)。 すなわち患者数はr=2で、発端者が1人(a=1)と第2症例が1の組数n₂₁=108、それに二人とも発端者（a=2）の組数はn₂₂=84であった。確認の確率の最尤推定値πとその誤差ｓが求められている(Yasuda 1979)。π=2n₂₂/(n₂₁+2n₂₂)、s=2√{n₂₁n₂₂(n₂₁+n₂₂)}/(n₂₁+2n₂₂)²}}。確認の確率はπ=0.608±0.034となる。

このモデルは同胞の患者数rで、そのうち発端者数aの核家族のデータに拡張できる。罹患きょうだいr人のうちa人が発端者とする。そうするとr-a人が第二症例である。発端者がいない罹患きょうだいは標本として上がってこないから、このときの発端者の分布は 

　　　　　　　　P(a|r)= _rC_aπ^a(1-π)^r-a/{1-(1-π)^r}　　　a=1,2,3,…,r 

で与えられる。このときπの最尤推定値を求めると 

　　　　　　　　　π=π+ U/K 、  s=√K 

である。ここでn_rを罹患者r人のきょうだい数とすると 

　　 　　　U=[A -��A_rn_r]/{π(1-π)}、  K=��B_rn_r/{π(1-π)}² (r=1,2,3,…) 

ただし A=��a・n_rsとB=��n_rsとである。n_rsはr人のうちa人の発端者がいるきょうだい数である。このデータはいわゆる(r,a)テーブルの形でまとめることができる。πの値はフィッシャーの推定値を最初に用いて上の式で反復計算をして求める。

　Furusho & Yasuda(1973)はある調査で次の(r,a)テーブルを得た。 

表4.1.1. 健常な両親から生まれた先天性聴覚障害者の(r,a)テーブル

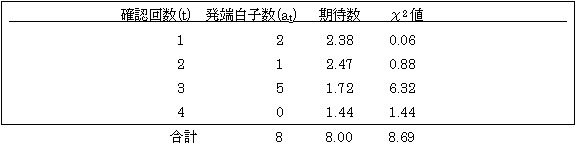
確認の確率の最尤推定値は π=0.5661±0.0010。(2人きょうだいからの値0.608±0.034と比べると誤差の範囲で二つの推定値は若干重なっている)。

例題 4.1.2. ある地区の集団の小児ダウン症をモニターしてその集団での発生率を求めたい。外表奇形診断(1)と染色体検査(2)をそれぞれ別のセンターで独立に行うものとすると、ダウン症と診断された小児は(1)か(2)のいずれかの検査によるか、両方(1 & 2)の検査によることになる(表4.1.2)。 

           表4.1.2. ２施設(方法)で発端者を確認するときの分布 

　　　　　　 　施設(方法)　　発端者数　　予測発端者数 

(1)             n₁       n[π₁(1-π₂)]/π

(2)             n₂       n[π₂(1-π₁)]/π       π=π₁+π₂-π₁π₂

               (1)&(2)         n₁₂      n[π₁π₂]/π   

                               n                         

各施設(方法)での確認の確率は 

　　　　　　　π₁=n₁₂/(n₂+n₁₂) ± √[{π(1-π₁)π₁}/(nπ₂)]

     　　　　 π₂=n₁₂/(n₁+n₁₂) ± √[{π(1-π₂)π₂}/(nπ₁)]。 

　集団全体での確認の確率πの最尤推定値とその誤差は次の式で与えられる。 

　　　　π=(nn₁₂)/{(n₁+n₁₂) (n₁+n₁₂)} ±π√[{(1-π)(π-π₁π₂)}/(nπ₁π₂)]。　

　このシステムでは重複して確認される発端者がいなければ(n₁₂=0)、πの値はいずれもゼロとなり、これは単独確認(π=0)に相当する。またこのシステムは適合度検定のための自由度がないので、2つの方法が独立であるという帰無仮説を検定することができない。3つ以上の方法を用いるなら可能となる(Yasuda 1979)。

　スエ―デンでのダウン症候群のモニタリングで、 (1)先天異常モニタリングと、(2)細胞遺伝学的検査の登録が行われた(Morton & Lindsten 1976)。これによると、n₁=52、n₂=127、n₁₂=231の登録があった。これよりπ₁=0.645±0.025、π₂=0.816±0.023、π=0.934±0.010が得られる。細胞遺伝学的検査の方が外表奇形の診断よりダウン症候群の確認確率が高いことが分かるが、これはとりもなおさず後者の検査の疾患診断精度が高いことを反映していると言えよう。全体の確認確率が93パーセントに達していることも興味深い。

例題4.1.3.　この切れた分割表truncated contingency tableモデルは切れたポアソン分布による連続モデルで扱うこともできる(Morton 1959、Yasuda 1979)。切れた分割表モデルとの違いは発端者が重複して確認される点で同じだがそれぞれの確認の確率の相違は問わずそれらの代表値として平均値で表す。患者を確認する無数の方法(施設)が沢山あって、疾患がまれであれば確認されるならポアソン分布で近似できる。ただし各回の確認は独立であると仮定する。発端者当たりの平均確認回数をmとすると、π=1-e^-mで表すことができる。確認回数(t)の分布は

 　　　　　　　　　　P(t)={ e^-m /(1- e^-m)}{m^t/t!} 

これを確認の確率πであらわすと 

　　　　　　　　　　P(t)={π/(1-π)}[{-ln(1-π)}]^t/t!    (t=1,2,3…) 

確認の確率の最尤推定値πはつぎの関係を満たす。 

　　　　　　　　　　-ln(1-π)/π=��ta_t/��a_t 

ここにa_tはt回独立に確認された発端者数である。この式の右辺は平均回数mの推定値に相当している。推定値の標準誤差は{1/√(��a_t)}・[ π/(1-π)]/ [√{(1/m)- (1-π)}]となる。mが1.1以下であればπ=2(m-1)と近似できる。

　白子についてあるアンケート調査(Tanaka & Watanabe 1967)で次の結果を得た。 

　　　　　　　　　　　表4.1.3. 各白子の確認回数の分布

    m=��ta_t/��a_t ={1×2+2×1+3×5}/{2+1+5}=2.375。したがってπ=0.87±0.07。

3回確認されている白子が5名いることは各回の確認が独立に行われていないことを示唆するもので、したがってこのπの推定値が過大評価されているとみられる。そのため有病率は過小推定となる。調査地区の人口が当時172,273名であったことを勘案すると、P=(5.3±1.1)x10^-5 (1万人に6名) という値が得られる。実際にはこれより多いと推察される。

4.2. いくつかの遺伝様式

　考えられる遺伝様式mode of inheritanceの種類には際限がないが、実際問題としてそのうちの僅かのモデルがテストできるに過ぎない。許容できるモデルに要請される性質として支持性support、経済性economy、解明性resolutionが挙げられる。支持性は手許のデータと適合することで、χ²や尤度比などの基準で判断する。経済性は仮説に含まれるパラメータの数が他に考えられる仮説のそれよりは多くなく、それに検定に用いる自由度が大きいほどよい。データが同じ数のパラメータを含む別のモデルを排除できるモデルを解明性という。穏当なモデルは別の集団での調査でもデータとよく合うものである。

古典的な分離比分析はまれなメンデル性疾患で症状が重篤な場合には不連続型変異モデル、混合型モデルはオリゴ遺伝子が関与する形質に、さらにポリジーンによる連続形質はしきい値モデルが妥当である。

　　　　モデル　　　　　健常と異常の分布様式　　　　　　　 　  異常の例　　

患者と健常者とに2分できた表現型データから、集団頻度、配偶者、きょうだい、それに親子の対から多くの情報が求められる。このとき最大4つのパラメータで済ますことができる。量的データでは環境指標の推定でパラメータ数は、遺伝と関係ない補助変数は別としても、有用と考えられるものだけでも倍増する。

　このような限界があるので、次の4つのモデルが使えよう。(i) 3つのパラメータを含む一般化した単一座位、(ii) 3~6個のパラメータを含む相加的な文化伝達モデル、(iii) 2つのパラメータを含む相加的な多因子遺伝モデル、それに(�C) (i) 〜(iii)の混合モデルではさらにパラメータは2つ以上追加して増える。

　これらの範疇に入らないモデルとして非因子結合型システム、複対立遺伝子、相加的でない複数座位などが多々考えられるが、データでこれらのモデルの厳密な検証は難しくなる。より簡易なモデルの有用性としては次が上げられよう。(i)データに合うという点で経済性がある。(ii)遺伝性と文化伝達とに分けられる、(iii)容認できる仮説で遺伝相談の予測ができる、(�C)連続変異から主要座位を取り出すことができる、それに(v)病因の異質性を調べることができる。経験的にいうと最後の2つでは家系調査が必須であるが、(�@)-(�B)の目標については対の血縁者は有用である。

4.3　単一座位の一般化

常染色体の1遺伝子座に2つの対立遺伝子A_1、A₂を想定する。3つの遺伝子型の量的形質それぞれの平均値を3つのパラメータで表す。

ここに、zはA₁A₁の平均値、tは2つのホモ接合間の差、dは優性の度合い(0≦d≦1)である。A₁とA₂の効果が相加的ならd=1/2でドミナンスがないno dominanceという (dの値は負になることもある：負の超優性) 。

完全混合を仮定し、突然変異や選択の存在を無視すると、集団の遺伝子型頻度はA₂の頻度qで決まる。親から子どもへの伝達transmissionはメンデルの法則にしたがう。すなわち遺伝子型A₁A₁、A₁A₂、A₂A₂の親からA₂で代表される配偶子の伝達確率はそれぞれ0、1/2、1である。年齢、性、その他の観察できる変量で決まる離散型リスク階級が定義されるなら、これらの効果は主座位について相加的である。i番目のリスク階級のホモ接合の平均をz_iとする。ここにiは易罹病性指数liability indexという。量的形質のデータが相加性であるとは定義として連続易罹病性の考えを暗黙に認めることになる。

　主座位の他に環境変量の相加的効果が考えられる。複数座位と文化伝達cultural inheritanceによる効果は無視する。すなわち

　　　　　　　　　　　　　　　x=g+e

ここでxは易罹病性、gは主座位効果、eは環境効果である。i番目の易罹病性指数についてgの値はz_i、z_i+dt、z_i+tの値をとり、eは平均ゼロ、分散Eの正規分布にしたがうものとする。gへのi番目の易罹病性指数の寄与は

　　　　　　　　　　　　　　μ_i= z_i+qt{2+q(1-d)}

で、その分散はG_i=q²(z_i+t)²+2q(1-q)(z_i+dt)²+(1-q)²z_i²-μ_i²。以上の前提から、G_iはすべてのiについて定数Gで、易罹病性クラスの分散VはG+Eと表される。Vとμ_iはデータから求めることができ、z_iはμ_i、d、t、qで表すことができるので、このモデルは3つの遺伝的パラメーター d、t、qで決まる。易罹病性を測る尺度として分散Vを1とし、一つのz_iをゼロとする。

　単一座位モデルの重大な限界に、他の遺伝様式あるいは文化伝達の特異的な検定ができないことが挙げられる。それは混合モデルの特別の場合となるため、家系データで検定できたとしても対の血縁者データでは結論を得られないことがしばしばある。仮によく合ったとしても、証明にはならないから注意深く家系データを集めて結論を導かなければならない。それでも求めた推定値を遺伝相談で慎重に用いることはできよう。しかし対の血縁者のデータが単一座位モデルに適合しなかったら、当然家系データを集めるべきではなく、遺伝相談に使用することもお勧めできない。

　残念ながら多くの疾患で、対の血縁者データは量、質ともに不十分である。発端者の定義が不明瞭なことやリスク推定の効率の悪さはデータとしての信頼度を下げる。様々の血縁度の対をまとまった数量として集める機会は少なく、十分な標本の大きさを得ることが難しい。したがって血縁者の対はよりよいデータを得るまでの推測でしかない。遺伝疫学者はデータに必要な情報をすべて取り出すよう努めなければならないが、事実を誇張しないように配慮しなければならない。

4.4 遺伝と文化伝達

　多くの形質は主座位の存在のヒントすらないのだが、家族間の環境変異の無作為性が疑われることがある。より正確に定義した表現型について適切な家系分析を行い、主座位を探すことができない場合次の線形モデルを考えてみるのもよかろう。

　　　　　　　　　　　　　　x=g+b+e

ここにxは易罹病性、gは平均0、分散G の相加的ポリジーンの寄与、bは平均0、分散Bの家族内の環境変異、eは平均0、分散Eの無作為の環境変異である。この3つの変量は正規分布をして、どの表現型についても相関がないとする。分散の合計はV=G+B+Eである。このモデルでG は遺伝(伝達の)変異を表す分散でありBは文化伝達変異の分散である。これは混合モデルでの主座位がない特殊の場合となっている。

　線形モデルを経路図path diagramで表わし、矢印は原因から効果へ、その経路係数path coefficientは標準化した偏回帰係数partial regression coefficientで表わす。未測定の変量は(楕)円形で、測定変量は矩形で表すことにする。

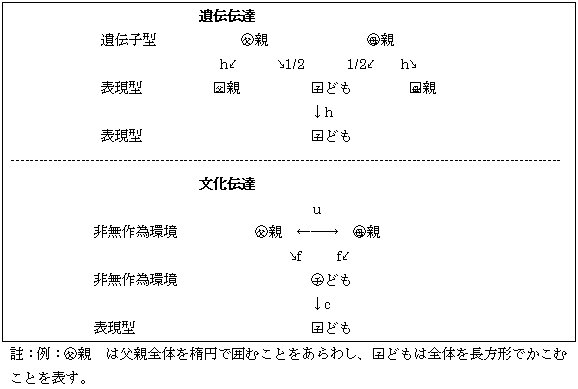
             図4.4.1. 遺伝伝達と文化伝達の簡単なモデル

　図4.4.1はパラメータhと係数１/2は遺伝伝達を示している。遺伝率h²は相加的因子による分散の割合である。図4.4.1ではh²=G/Vである。この簡単な遺伝モデルでは親子間の遺伝率は、あたかも同年齢で測定したとして一定であるとしている(表4.4.1.)。親の遺伝子型間には相関がないとしている。係数1/2は子どもの遺伝子の半分が片親から由来しているから、子どもと片親の相関係数は１/2である。子どもの遺伝子型の(1/2)²+(1/2)²=1/2が両親との相関で説明できる。残りの1/2は親の配偶子の分離の際の偶然であって、二倍体の生物ではそれぞれが1/２となる。

文化伝達にはパラメータu、f、cが関与している(表4.6.1)。無作為でない環境変異は家族員の間の相関による環境変異で、配偶者間の相関はuである。子どもの作為的な環境変

　　　　　     　  表4.4.1. いくつかの集団での収縮期血圧

異はその一部が親の作為的な環境変異で決まるが、変数fは遺伝伝達の1/2に相当する。子どもの作為的な環境変異の分散の一部2f²(1+u)は両親で決まる。より一般的に、父親、母親それぞれの経路係数f_Fとf_Mは無作為でない環境変異の違いで決まる。文化(伝達)率cultural heritability cは無作為でない環境変異の割合で決まる子どもの表現型分散の割合でc²=B/Vで表わす。

　以上の事柄は経路係数の次の２つの規則にしたがう。

1.      原因から効果への関係は一方向矢印であらわす。二方向矢印は分析外の相関に用いる。p_ijでjからiへの因果経路causal path、r_jkをjとkの相関を表わす。そうすると、iとkの単純相関は

　　　　　　　　　　　　r_jk=��p_ij r_jk= p_i1 r_1k+ p_i2 r_2k+･･･

　 で表せる。これらから因果経路の矢印の方向は決して同じ原因に向うことはない。

2. 経路図にないがiに作用するすべての要因、それらとは相関がないことによる残りの経路をp_iuとする。そうすると完全に決まるcomplete determination。

　　　　　　　　　　　　��p_ij r_jk+ p_iu²=1

�狽ﾍjについての和を表す。無作為な環境は残りの経路の一つである。残りの経路は通常経路図に書かない。それは上式から

　　　　　　　　　　　　p_iu=√(1-��p_ij r_jk)

で表わせるからである。　一般に遺伝への応用では、すべてのi、jについて

　　　　　　　　　　　　0≦p_ij≦1、　-1≦r_ij≦1

である。

　経路分析path analysisはS. ライト(Wright 1968)が遺伝疫学と類似したデータの因果関係の分析の一方法として開発した。経済的で最も少ないパラメータの線形モデルを取り上げてその結果を導く方法としてこれが最良である。そしてこれらの仮定を対の血縁者などの相関関係を用いて検定することができる。経路分析は独立変数の誤差を容認した重相関の特別の場合であるので、別法として相関に関する尤度比でも因果モデルの検定が行なえよう。

4.5. 同類交配

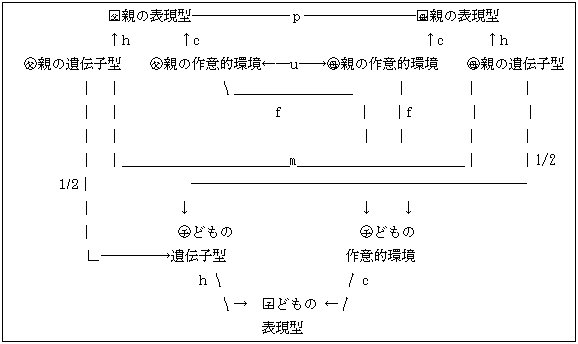
　遺伝疫学で扱う多くの表現型で同類交配に関わる可能性はあまりない。配偶者となる前の2人はお互いの遺伝子型、罹病性、あるいは生化学的な構成についての知識はないのが普通である。したがってそのような形質の配偶者相関は婚姻後の要因、共通の食事、習慣、病気への暴露などに依存するのであろう。血圧、血清コレステロールなどの結構誤差の大きい測定値が関与する形質については、通常の家族員の調査で特定の調査者が同時に行なうとみかけの相関を生じることがある。遺伝疫学者は時間と調査者を確率化してそのような観察者効果を避ける努力を払う必要がある。また、このような注意を払っていない古いデータを扱うときには慎重でなければならない。行動形質や人類学的形質の一部にはかなりの配偶者相関が見つかることがある(IQや身長など)が、これは一部に婚姻前の組合せ、すなわちホモガミーhomogamyによることがある。この場合お互いの配偶者は他方に原因があるのではなく、一方の性がまったく無作為に他方の性を選んでいるわけでもない。特別の記号と相互に選ぶことが計算上必要である。そのためクロニンジャー(Cloninger 1980)は共通経路co-pathという考えを開発した。これは矢印を取り除き、相互の要因はお互いに独立で一対の原因に特異的な偏相関があるとするものである。共通経路は取り上げた変量が原因か結果に関わらないで両方向に起因するもので、従来の経路分析の一方向と二方向矢印とは論理的に異なるものである。

　図4.5.1.は配偶者の表現型(表現型ホモガミー)間の共通経路ｐと配偶者の作為的な環境(社会的ホモガミー)の相関uに配慮した同類交配を図示したものである。表現型ホモガミーは常に婚姻以前の要因によるが、社会的ホモガミーは婚姻前、婚姻後、あるいは両方の要因によるかもしれない。婚姻前の社会的ホモガミーは社会階級、宗教、地理、あるいは生活様式の違いによる同族内の諸要因などに分割できる。婚姻後の社会的ホモガミーは同棲期間あるいは観察者の偏りまたはその両者によることもあろう。

　婚姻前に属する民族の相違、社会的階級の遺伝的分化、婚約者が特定の疾患の施設に収容されていたなどで、社会的ホモガミーは原則的に配偶者の遺伝子型間の相関mを生じると考えられるが有意となる例はこれまで報告が見当たらない。これは明らかに民族、環境の相違についての対の血縁者の調査は一般に避けてきたことにもよろう。

以上は相違と性差を抜きにして単純化した因果関係である。多くの場合、親と子どもを異なる年齢で観察するなら、測定値は同じではない。この事実を取り入れるために、子どもと成人の遺伝的経路や文化的経路を区別する必要がある。また環境と両親の組み合わせ

　　　　図4.5.1. 表現型ホモガミー(p)と社会的ホモガミー(u,m)のある同類交配

で胎児あるいは幼児への効果に性差があるかもしれない。このような世代間あるいは性の違のある場合についての経路図が工夫されている。

4.6. 量的形質

　調査した連続確率変数は分析の実行に際して、年齢、性、家族の類似性と無関係と考えられる変量について標準化するため、歪度を少なくする予備的な変換(対数変換、平方根変換など)をする。その際、外れ値outlierとなる観察値は測定の誤りと思われるなら取り除く。

回帰モデルを取り上げてみよう。

　　　　　　　　　　　　　　X=A+��b_iZ_i+ε

ここにXは従属変数、Zは年齢、性、年齢×年齢などの独立変数、そしてεは平均0、分散σ²の正規変量である。そうすると

　　　　　　　　　　　　　　ｘ＝(X-A-��b_iZ_i)/σ_x

σ_xはA+��b_iZ_iで決まる(xの属する)階級の標準偏差である。そして冪変換で尖度を削り、歪度を少なくする(ボックス・コックス変換)。このような操作をデータに加える目的は要因とは無縁の因子から予測できるものを除き、ほぼ正規分布標本に近づけることにある。

　ときおり標本収集のきっかけが発端者であるとき、極値の発端者が選抜の基準となることがある。このような確認法に由来する偏りは補正しなければならない。対の血縁者の場合には、発端者への回帰を行なうのが最上である。このとき

　　　　　　　　　　　　　　　　r_ij=b_ij(σ_j/σ_i)

の関係を用いる。この式の回帰係数は発端者の選抜により偏ることはないし、σ_j、σ_iは一般集団の標準偏差である。発端者が複数いる場合の偏りの補正法についてはまだ完全に解決していない。

　標準化と冪変換の後、量的形質Pは社会的階級、健康のための運動、食事、喫煙、アルコール量などの生活スタイルをあらわす変量zから予測することができる。重回帰モデル

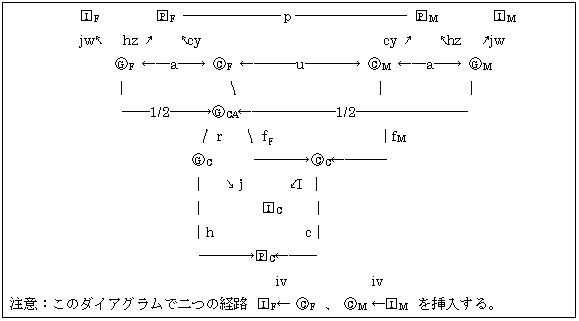
図4.6.1. 同類交配、指標、母性効果それに世代間の相違があるときの家族類似性

　　　　　　　　　　　　　　　P=a+��b_iz_i+ε’

からPの指標としてI=��b_iz_iが得られる。

図4.6.1.は指数だけでなく他の複雑性をも含む経路ダイヤグラムである。添え字F、M、Cは父親、母親、子どもを表わしている。添え字CAは成人した子どもである。　表現型

Ｐと指標Ｉの組になる観察値は遺伝子型Gと作為的な環境Cで決まる一部分である。無作為な環境で決まる残りの経路はここには示していない。世代間の相違によるものは表現型(y、z)と指標(v、w)の経路に取り込んである。遺伝子・環境の相関aが親子で一定であれば、それは独立ではなく他の経路係数の関数である。

　　　　　　表4.6.1. 混合型ホモガミーモデルにおけるパラメータの定義

　このモデルは複雑なように思えるが、両親と子どもで構成された核家族nuclear familyで完全に決まる。養子、一卵性ふたご、半きょうだい、一卵性ふたごの子ども達、それに遠い血縁者などのまれな血縁関係からも情報が得られる。核家族は最も有意義な血縁関係であるので、遺伝疫学者は核家族の指標にまず集中するのがよいかもしれない。あるいは、指標は無視して、稀なあるいは遠縁の血縁関係のデータを集める。この場合、ふたごの社会的つながり、あるいは養子の選択的交換などの特異的要因が通常の家族類似性を乱すがそれを外挿するかもしれない。最もよい方法は研究の主目的を指標に置いて核家族を調査する。それと共に稀なあるいは遠縁な血縁を調べて、モデルの付加テストを行なうのである。

　データは一つの集団を同一研究者によって調査するのが理想である。実際、調査や集団の間で多くの変異がある。いくつかの調査データを一つにまとめるときは、反復調査による分散は不適切な適合度のχ²検定を行うより、F検定での誤差として扱うべきである。

　このモデルでの分散成分の推定は世代間の相違と母性効果であることが示されることがよくある。文化伝達にはよくあることで、ときには遺伝(伝達)よりも家族類似性を定めるより重要決定因子となることがある。家族類似性の遺伝成分を表わす適切な尺度R_Gは

　　子どもについては　　　　　  (h²/2)/(c²+ h²/2)

　　成人については　　　　　　　(h²z²/2)/(c²y²+ h²z²/2)

である。なぜなら、すべての文化伝達と半分の遺伝(伝達)が家族類似性に関わるからである。

4.7. 罹患性

　量的形質Xはしきい値threshold Zでデータを二群に分けることができる：X＜Zならば「健常」、X＞Zならば「罹患」である。Xが平均μ、分散σ²の正規分布に従うなら、罹患する確率は

P(患者|X)= (1/√2π)∫e-^x2/²dx≡Q(x)

ここでx=(X-μ)/σ、z＝(Z-μ)/σである。積分は[x, ∞)の範囲である。これはコンピュータで数値計算をして求めことができる。

　量的形質を健常と罹患の二群に分けることで、個々の個体がしきい値にどれほど近いか遠いかの情報を失うことになる。この情報の損失は量的形質の正規性からのずれを心配しなくてもよいとする便法を上回る。さらに共分散分析よる余分の変異あるいはXと線形の指数を導入する必要もない。その代わり健常者0、患者1を年齢、性、それに他の要因に回帰することで判別が可能となるであろう。

量的判別はXへの非線形であるから、罹患リスクの大きくなる順序においていくつかの階級i=1、…、nに多分割するとよい。ここでiは易罹病性指数である。これから

　　　　　　　　　  　P_jkl=P(個人_j|血縁者_kl=罹患)

ここでj､k､lは易罹病性指数、lは血縁関係の種類である。この確率はl、a_j、a_kと量的形質の相関係数の複雑な関数である(表4.7.1、表4.7.2)。対の血縁者を独立標本とみなすと、その尤度は

　　　　　　　　　　　L=ΠP_jkl^rjkl(1-P_jkl)^cjkl、

ここで集合ijkについてr_jklは患者数、c_jklは健常者数を表す。

　以上のモデルは計算量が増えるが、考えは簡単である。量的形質を観察してそれを二分するか、あるいはモデルのさまざまな要因の作用が線形である単に抽象的な易罹病性の尺度であるかは適宜判断する。このようなモデルから指数特異性の浸透率も主座位について求めることができる。

　 表4.7.1. 　9つの血縁関係で確定診断のついた統合失調症の観測値と期待値

(発生率は0.85%)

　　　　　　　　表4.8.2. 統合失調症についての仮説と推定値

3種類以上の表現型に分割することで罹患者からより多くの情報を得ることができることがある。頻度分布として対数正規分布にしたがう変量Xを取り上げてみよう。3分割では真中のクラスは健常と患者の間(境界型?)でもよいし、患者に含めてもよい。前者はM<X<Zで後者はX>Mである。ここにZははっきりと患者であることを示すしきい値、M は境界型を定義するしきい値である。Xを観察して三分割できたとき、あるいは境界型の表現型が患者の症状と違っているときのモデルであろう。後者は境界型の一部が患者である場合のモデルに適切であろう。

4.8. 参考文献

Cloninger CR　1980. Interpretation of Intrinsic and Extrinsic Structural Equations by Path Analysis. Theory and applications to Assortative Mating. Genet Res 36:133-145.

Crow JF 1965. Problems of Ascertainment in The analysis of Family data. In Genetics and the Epidemiology of Chronic Diseases (Eds Neel JV, Shaw MW, Schull WJ). US Department of Health, Education, and Welfare. Washington DC. Pp. 23-44.

Furusho T & Yasuda 1979. Genetic Studies of Inbreeding in Some Japanese Populations �]�V. A Genetic Study of Congenital Deafness. Jpn J Human Genet 11:1-16.

Haldane JBC, 1964. A Defense of Beanbag Genetics. Perspective in Biology and Medicine 7: 343-359.

Li CC 1975. Path Analysis. The Boxwood Press, Pacific Grove.

Morton NE, 1959 Genetic Tests Under Incomplete Ascertainment. Amer J Human Genet 11:1-16.

Morton NE & Lindsten J. 1976. Surveillance of Down’s Syndrome as a Paradigm of Population Monitoring. Human Hered 26:360-371.

Reich T, James JW, Morris CA 1972. The Use of Multiple Thresholds in Determining the Mode of Transmission of Semi-continuous Traits. Ann Hum Genet 36:163-184.

Rao DC, Morton NE, Cloninger CR. 1979. Path Analysis Under Generalized Assortative Mating. I. Theory. Genet Res 33:175-188.

Rao DC, Morton NE, Gottesman II, Lew R. 1981. Path analysis of attribute data on pairs of relatives. Application to Schizophrenia Hum Hered 31:325-333.

Wright S. 1968. Evolution and the Genetics of Populations. I. Genetic and Biometric Foundations. University of Chicago Press, Chicago, 1968.

Yasuda N. 1979. Estimation of the Ascertaiment Probability of Rare Diseases. Jpn J Human Genet 24:265-291.